Network Topologies and Routing

Network Topologies and Routing

We here give a brief introduction to specifying different topologies and routing strategies. We will only discuss one basic example (torus). A more thorough introduction covering all topologies is planned for future releases. Excellent resources are "Principles and Practices of Interconnection Networks" by Brian Towles and William Dally published by Morgan Kaufman and "High Performance Datacenter Networks" by Dennis Abts and John Kim published by Morgan and Claypool.

Topology

Topologies are determined by two mandatory parameters.

topology_name = torus
topology_geometry = 4 4

Here we choose a 2D-torus topology with extent 4 in both the X and Y dimensions for a total of 16 nodes (Figure 2) The topology is laid out in a regular grid with network links connecting nearest neighbors. Additionally, wrap-around links connect the nodes on each boundary.

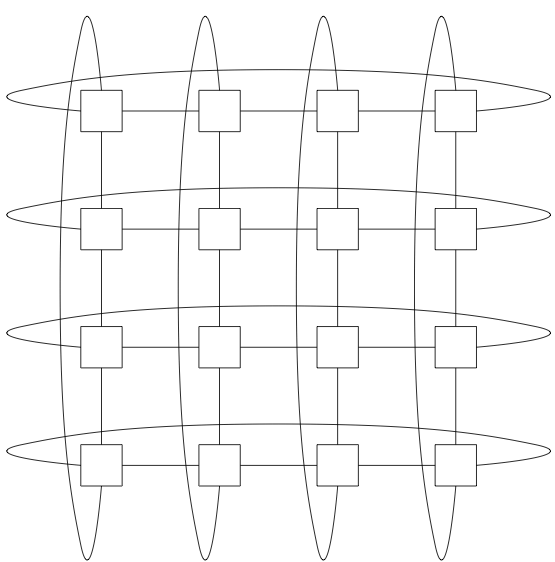
Figure 2: 4 x 4 2D Torus

The figure is actually an oversimplification. The topology_geometry parameter actually specifies the topology of the network switches, not the compute nodes. A torus is an example of a direct network in which each switch has one or more nodes "directly'' connected to it. A more accurate picture of the network is given in Figure 3.

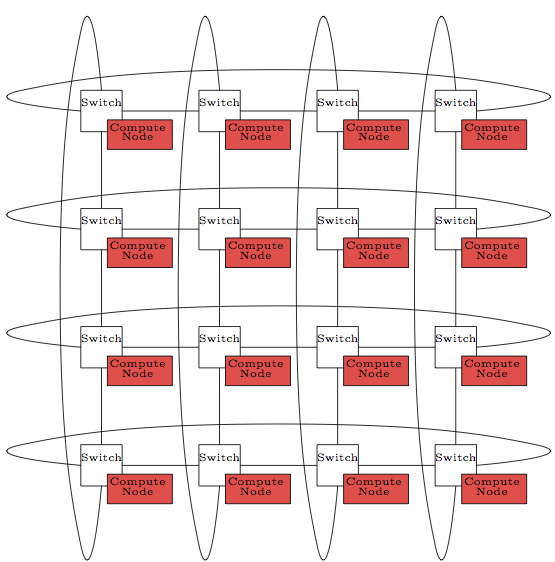
Figure 3: 4 x 4 2D Torus of Network Switches with Compute Nodes

While in many previous architectures there was generally a one-to-one correspondence between compute nodes and switches, more recent architectures have multiple compute nodes per switch (e.g. Cray Gemini with two nodes). Multinode switches can be specified via

topology_name = torus
topology_geometry = 4 4
network_nodes_per_switch = 2

which would now generate a torus topology with 16 switches and 32 compute nodes.

Another subtle modification of torus (and other networks) can be controlled by giving the X, Y, and $Z$ directions different bandwidth. The above network could be modified as

topology_name = torus
topology_geometry = 4 4
topology_redundant = 2 1

giving the the X-dimension twice the bandwidth of the Y-dimension. This pattern DOES exist in some interconnects as a load-balancing strategy. A very subtle point arises here. Consider two different networks:

topology_name = torus
topology_geometry = 4 4
topology_redundant = 1 1
network_bandwidth = 2GB/s

topology_name = torus
topology_geometry = 4 4
topology_redundant = 2 2
network_bandwidth = 1GB/s

For some coarse-grained models, these two networks are exactly equivalent. In more fine-grained models, however, these are actually two different networks. The first network has ONE link carrying 2 GB/s. The second network has TWO links each carrying 1 GB/s.

Routing

By default, SST/macro uses the simplest possible routing algorithm: dimension-order minimal routing (Figure 4).

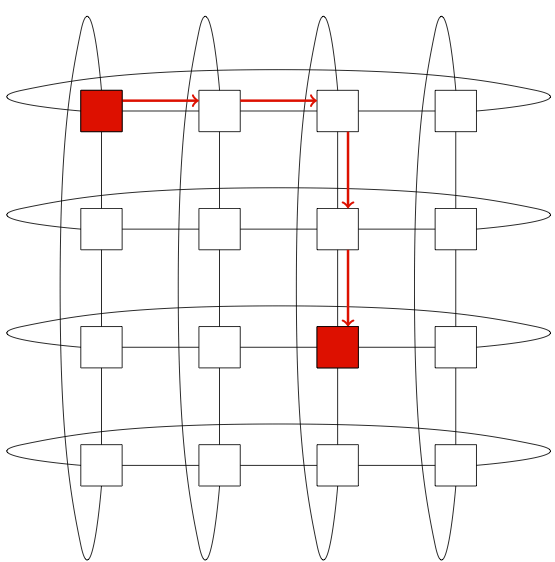
Figure 4: Dimension-Order Minimal Routing on a 2D Torus

In going from source to destination, the message first travels along the X-dimension and then travels along the Y-dimension. The above scheme is entirely static, making no adjustments to avoid congestion in the network. SST/macro supports a variety of adaptive routing algorithms. This can be specified:

router = min_ad

which specifies minimal adaptive routing. There are now multiple valid paths between network endpoints, one of which is illustrated in Figure 5.

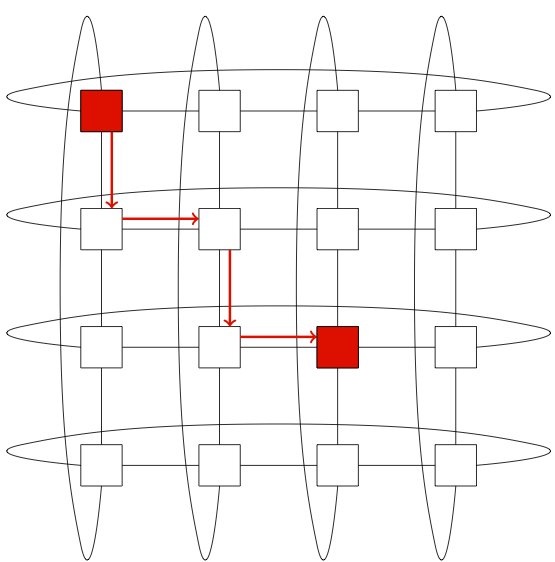
Figure 5: Adaptive Minimal Routing on a 2D Torus

At each network hop, the router chooses the productive path with least congestion. In some cases, however, there is only one minimal path (node (0,0) sending to (2,0) with only X different). For these messages, minimal adaptive is exactly equivalent to dimension-order routing. Other supported routing schemes are valiant and UGAL. More routing schemes are scheduled to be added in future versions. A full description of more complicated routing schemes will be given in its own chapter in future versions. For now, we direct users to existing resources such as "High Performance Datacenter Networks'' by Dennis Abts and John Kim.